Степенная функция с комплексным показателем

(19)

В частности, если взять главное значение логарифма (k = 0), то получим главное значение степени :

.

Отдельные ветви степенной функции, то есть однозначные функции (19), являются регулярными функциями на плоскости с разрезом вдоль отрицательной части вещественной оси, так как их можно там дифференцировать по обычному правилу.

Общее определение степенной функции указывает на то, что эта функция бесконечнозначна. Однако некоторые частные виды степенной функции являются функциями однозначными или же многозначными, но не бесконечнозначными, как следовало бы из (18). Например, известно, что функция , где - натуральное, одночлена, так как она получается независимой переменной с помощью однозначного действия умножения. Функция многозначна, но известно, что каждому значению отвечает ровно различных значений. Выясним, как эти известные факты получаются из общего определения (18).

а) Пусть . Исходя из определения (18), получаем:

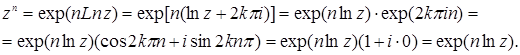
полученное выражение не содержит и, следовательно, функция однозначна.

б) Пусть . В силу определения (18) получаем:

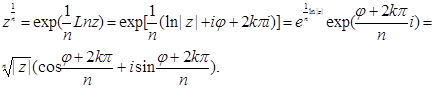(20)

Из последнего выражения видно, что при изменении от 0 до будем получать разные числа в скобках. При дальнейшем изменении от до числа, получающиеся в скобках, будут повторяться в силу периодичности синуса и косинуса. Например, при , получим:

,

то есть пришли к тому же числу, которое уже было получено при .

Так же значение суммы в скобках при совпадает с там значением, которое было при и так далее. Если , то получим:

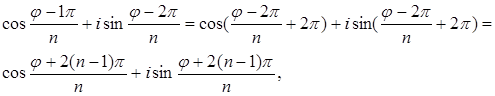
то есть то же число, которое уже было при ; при , получим то же число, которое уже было при , и так далее.

Итак, формула (11) даёт для каждого ровно различных значений функции, которые получаются, например, при .

При всех , отличных от и , где и целые, формула (18) определяет бесконечнозначную функцию [1].