Методика работы с геометрическими образами

Работа с геометрическими образами при усвоении математики предполагает значительную нагрузку на интеллект, поэтому «насыщение» урока учебным материалом, требующим работы с образом, должно опираться на четкое осознание учителем того, какой тип заданий он предлагает ученику.

Таких заданий в геометрии используется много. Они содержатся в учебниках, анализируются учителем на уроке, задаются в виде контрольных (самостоятельных) работ, как домашние задания. Они различаются своим математическим содержанием. Они неоднородны и по составу той реальной деятельности, которая обеспечивает создание по чертежу образов. Но именно с этой точки зрения задания в учебниках недостаточно систематизированы ни в пределах одной темы, ни курса в целом. Задавая их ученикам, учитель не всегда отдает себе отчет в том, какие требования они предъявляют к созданию образа. Конечно, образ возникает у ученика по чертежу (в большинстве случаев) адекватный, но как именно он возникает, этого, как правило, не знают ни авторы учебников, ни учителя. Констатируя конечный результат — созданный образ (правильный или неправильный), учитель не располагает набором заданий, который позволил бы ему «зондировать» сам процесс создания геометрического образа. Целесообразно различать две системы заданий (см. 4.1 и 4.2).

Эти задания широко используются в школьной геометрии. Они предполагают выполнение чертежа в соответствии с условием задачи, заданным в словесной или символьной форме. Есть такие задачи, которые задаются словами и не содержат ни букв, ни символов в тексте («Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок ее, заключенный между параллельными сторонами, делится в этой точке пополам»).

Пример1: Сделайте чертежи по условиям задач, используя данные в них обозначения:

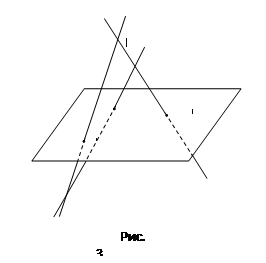
Прямая АВ пересекает плоскость α в точке М (рис. 1).

Плоскости α и β пересекаются по прямой МР, а плоскости α и γ пересекаются по другой прямой МТ (рис. 2).

Задания на выделение существенных признаков

геометрических понятий, их актуализацию

Выделение существенных признаков может осуществляться:

а) по словесному описанию условий задачи;

б) по графическому изображению фигуры.

Ученик по словесному описанию задачи должен выделить (подчеркнуть) те слова, в которых заключены существенные признаки понятий, опознать их; уметь дифференцировать словесно те условия (их совокупность), которые определяют, что «дано», а что «требуется найти» (доказать, вычислить и т.п.). Это необходимо, чтобы ученик мог сознательно отчленять известное от искомого. Вычленение существенных признаков понятий можно организовать и по чертежу.

Пример 2: На рисунке изображены три попарно пересекающиеся прямые, которые пересекают плоскость α. Верно ли сделан рисунок? (рис. 3)

Решение: При внимательном изучении рисунка видно, что прямые а, b и c лежат в одной плоскости (используется аксиома задания плоскости).

Прямые а, b и c пересекают плоскость α по прямой, на которой лежат точки А, В и С (аксиома пересечения плоскостей). Но по чертежу видно, что через точки А, В и С невозможно провести единственной прямой. Следовательно, рисунок сделан неверно.

Очень часто чертеж представляет собой не одну (однородную) фигуру, а их совокупность. Для решения задачи не все фигуры одинаково значимы. Необходимо зрительно выделить эту фигуру из состава других, мысленно ее «подчеркнуть»; удержать в образе, чтобы работать с ней. Для этого необходимо фиксировать внимание не на всех, а лишь на отдельных фигурах; причем на разных этапах решения задачи может происходить как бы смена «фигуры и фона»: те фигуры, которые рассматривались как значимые для решения задачи, должны сменяться другими. Для этого ученику нужно от них отвлечься, чтобы перейти к другим. Необходимы специальные упражнения, обеспечивающие возможность не только продуктивного выделения фигуры из фона, но и динамической смены их (то, что было «фоном» становится «фигурой», и наоборот). Такие задания полезны как в целях дифференциации учащихся, так и для развития у них умения последовательно, логично, обоснованно переходить в образах от одной фигуры к другой, подобно тому, как они учатся строго, логично, последовательно словесно излагать свои мысли. Переход от одной фигуры к другой в образах должен быть аргументирован опознаванием существенных признаков, детерминирован требованиями задачи.