Анализ учебного материала по теме «Квадратичная функция» в учебниках по алгебре 7-9 классов

Далее аналогично строится график функции и сравнивается с графиком функции . График функции может быть получен из графика функции с помощью симметрии относительно оси х.

Далее авторы, подводя итог, говорят, что графики функций и (при ) симметричны относительно оси х.

В конце этого параграфа говорится, что построение графика, симметричного данному относительно оси х, растяжение графика от оси х или сжатие к оси х – различные виды преобразования графиков функций. Преобразования графиков, рассмотренные для функции , применимы к любой функции.

Система упражнений на закрепление этой темы состоит из упражнений на построение графиков функций.

Затем авторы рассматривают графики функций вида и . В качестве примеров берутся другие частные случаи квадратичной функции.

Далее делается вывод: график функции является параболой, которую можно получить из графика функции с помощью параллельного переноса вдоль оси у на n единиц вверх, если , или на –n единиц вниз, если ; график функции является параболой, которую можно получить из графика функции с помощью параллельного переноса вдоль оси х на m единиц вправо, если , или на –m единиц влево, если .

Полученные выводы позволяют понять, что представляет собой график функции . Рассматривается очередной пример () и после этого делается вывод, что график функции является параболой, которую можно получить из графика функции с помощью двух параллельных переносов. Замечается, что производить параллельные переносы можно в любом порядке: сначала выполнить параллельный перенос вдоль оси х, а затем вдоль оси y или наоборот.

Далее в учебнике рассматривается построение графика квадратичной функции в общем виде. Вводится квадратичная функция и из трехчлена выделяют квадрат двучлена. После некоторых преобразований авторы получают 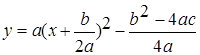. Получается формула вида, где , 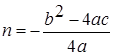. Авторы акцентируют внимание на том, что график функции есть парабола, которую можно получить из графика функции с помощью двух параллельных переносов – сдвига вдоль оси х и сдвига вдоль оси у.

Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров, Н.Е. Федорова, М.И. Шабунин

7 класс

В 7 классе рассматривается прямоугольная система координат, понятие функции, линейная функция и ее график.

8 класс

В данном учебнике изучение квадратичной функции начинается в 5 главе после изучения квадратных корней и квадратных уравнений.

Сначала рассматриваются примеры из разных областей науки и техники, где встречаются квадратичные функции.

После этого вводится определение квадратичной функции, и рассматриваются примеры квадратичных функций и задачи.